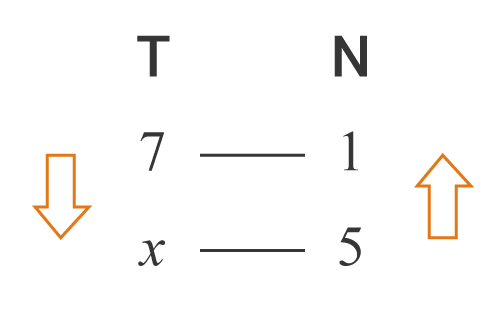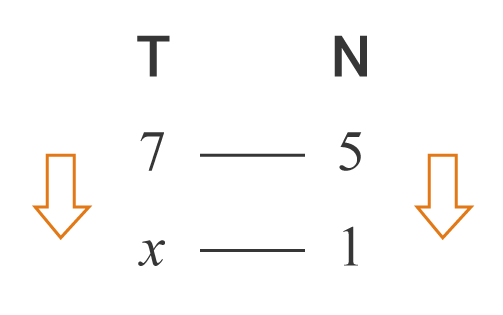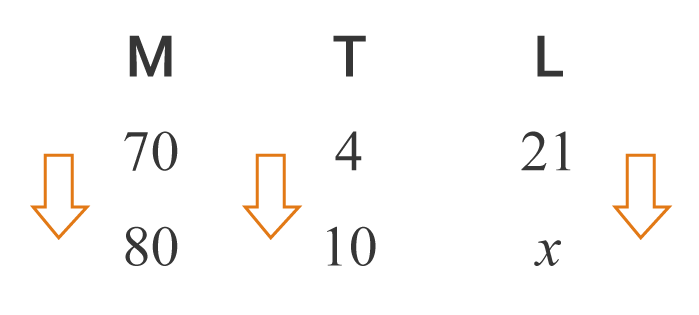Descrição
O estudo de equações do primeiro grau, razões, proporções, regras de três e juros.
PROPÓSITO
Apresentar a aplicabilidade dos conceitos matemáticos aqui explorados em situações do cotidiano e em contextos não escolares.
Preparação
Antes de iniciar o conteúdo deste tema, tenha em mãos papel, caneta e uma calculadora científica ou use a calculadora de seu smartphone/computador.
OBJETIVOS
Módulo 1
Examinar a importância das equações do primeiro grau
Módulo 2
Identificar razões, proporções e porcentagens
Módulo 3
Resolver problemas do cotidiano com regras de três
Módulo 4
Praticar problemas com juros simples e compostos
Introdução
MÓDULO 1
Examinar a importância das equações do primeiro grau
Introdução
Neste módulo, abordaremos como as equações do primeiro grau aparecem continuamente em problemas do cotidiano. Veremos como resolver tais tipos de problemas após uma análise e interpretação dos mesmos. Como exemplo do que trabalharemos, considere a seguinte situação:

(UFRRJ- 2003) Clarissa é uma típica consumidora de shopping. Seu pai lhe deu uma certa importância em dinheiro para que comprasse algumas coisas. Ao passar por uma sapataria, encantou-se com um tênis e pagou por ele um quinto do que recebeu de seu pai. Em seguida, entrou numa loja de roupas e comprou uma calça, pagando um quarto do que restou. Clarissa ainda ficou com R$120,00. Qual foi a quantia que ela recebeu de seu pai?
Como resolver esse tipo de problema?
Antes de iniciarmos com os estudos e resoluções desse tipo de situação, vamos entender o conceito de equação do primeiro grau.
Uma equação do primeiro grau é uma expressão matemática envolvendo termos conhecidos e desconhecidos da forma:
É importante destacar que existem outros tipos de equações do primeiro grau com várias incógnitas, porém, neste tema, abordaremos somente as equações do primeiro grau com uma incógnita apenas, como a equação acima.
Antes de iniciarmos a análise de situações-problema, vejamos o seguinte. Acredito que muitos já devem ter visto em alguma rede social alguns desafios semelhantes aos do vídeo a seguir:
Agora que percebemos como o nosso assunto pode estar implicitamente presente em alguns passatempos do dia a dia, vamos analisar outras situações. Veremos como essas situações nos fornecem equações do primeiro grau que podem ser resolvidas conforme comentamos anteriormente.
Agora, pegue papel, caneta e sua calculadora, pois você testará seus conhecimentos.
Em uma corrida de táxi, é comum pagarmos uma taxa fixa (chamada bandeirada) mais um valor variável que depende da distância percorrida. Se a bandeirada é de R$4,20 e o quilômetro rodado custa R$0,95, qual é distância percorrida por um passageiro que pagou R$21,30?

Vamos denotar por a quantidade de quilômetros rodados. Como a bandeirada (R$4,20) é fixa e pagamos R$0,95 por quilômetro rodado, então, se o passageiro pagou R$21,30 pela corrida, a equação do primeiro grau que representa essa situação é:
Logo, a distância percorrida pelo passageiro foi de 18km.
Na verdade, a situação também poderia ser resolvida com um raciocínio puramente aritmético. Subtraindo a bandeirada do total da corrida, obtemos 21,30 – 4,20 = 17,10. Dividindo este valor pelo custo do quilômetro rodado, obtemos 17,10/0,95 = 18 km. Observe que os cálculos efetuados correspondem aos passos de resolução da equação acima. A vantagem de formular o problema como uma equação do primeiro grau é ter um processo mais automático de resolução.
(Adaptado de UNIRIO– 2016) Um grupo de amigos vai acampar no final de semana. Numa certa hora da manhã de domingo, o equivalente a um terço desse grupo está envolvido com o preparo do almoço, a metade do grupo cuida da limpeza do acampamento, a décima parte desses dois subgrupos colhe flores na redondeza e a única pessoa restante do grupo deleita-se lendo um bom livro. Quantos elementos tem esse grupo de amigos?
Atenção: A imagem abaixo é meramente ilustrativa, não leve em consideração a quantidade de personagens presentes na cena para a resolução da atividade.
Vamos denotar por a quantidade de amigos nesse grupo. Pelas informações do exercício, temos a seguinte divisão do grupo:

- Um terço desse grupo está envolvido com o almoço .
- Metade do grupo cuida da limpeza .
- A décima parte dos dois subgrupos acima colhe flores .
- Um elemento do grupo lendo um livro .
Como todos os elementos do grupo estão distribuídos em uma das atividades acima, podemos formar a seguinte equação do primeiro grau:
Vamos voltar à situação mencionada no início deste módulo:
Clarissa é uma típica consumidora de shopping. Seu pai lhe deu uma certa importância em dinheiro para que comprasse algumas coisas. Ao passar por uma sapataria, encantou-se com um tênis e pagou por ele um quinto do que recebeu de seu pai. Em seguida, entrou numa loja de roupas e comprou uma calça, pagando um quarto do que restou. Clarissa ainda ficou com R$120,00. Qual foi a quantia que ela recebeu de seu pai?
Vamos denotar por a quantia em dinheiro que Clarissa recebeu de seu pai. Utilizando as informações do exercício, temos o seguinte:
1º gasto
Na sapataria, gastou um quinto da quantia total
Restou
2º gasto
Com a calça, gastou um quarto do que restou
Restou ainda R$120,00.
Com as informações acima, temos que a quantia total de dinheiro é igual à soma dos gastos mais o valor que sobrou, R$120,00. Assim, formamos a seguinte equação do primeiro grau:
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 2
Identificar razões, proporções e porcentagens
INTRODUÇÃO
Conforme comentado no módulo anterior, diversas situações do cotidiano envolvem tópicos da Matemática de maneira implícita, mas que podem ser resolvidos rapidamente após uma análise e interpretação do problema.
Neste módulo, abordaremos especificamente os conceitos de razões, proporções e porcentagem, juntamente com algumas das suas aplicações. Veremos que, em diversos contextos, esses conceitos nos fornecem informações que podem auxiliar, por exemplo, no planejamento de um transporte de cargas ou para se ter uma comparação sobre o aproveitamento escolar de uma turma. Por exemplo, considere a seguinte situação:

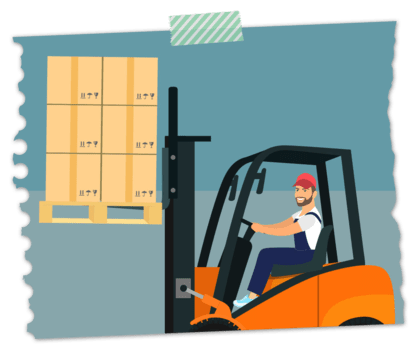
Sabendo que a capacidade de carga de um caminhão é de 10 toneladas e cada caixa do produto que será transportado pesa 200kg, qual a razão entre o peso de cada caixa e a carga máxima transportada?
Veremos como resolver o problema acima utilizando o próximo conceito.
Razão
A razão entre dois números reais e , onde ≠ 0, é o valor do quociente de por , que representamos das seguintes maneiras:
ou
As duas representações acima podem ser lidas dos seguintes modos:
- Razão de para ;
- está para ;
- para .
O termo nessas representações é chamado de antecedente e o termo é chamado consequente.
Sejam e números reais não nulos. A razão inversa (ou recíproca) da razão é a razão:
Note que .
Vejamos alguns exemplos de razões e os seus significados.
- A razão de 20 para 5 é um exemplo de razão cujo valor é 4, pois a razão de 20 para 5 é representada pelo quociente ;
- A razão de 10 para 30 é um exemplo de razão cujo valor é , pois a razão de 10 para 30 é representada pelo quociente .
Pegue novamente o papel, a caneta e a calculadora! Vamos praticar!
Digamos que o salário de Pedro é de R$4.000,00 e o de Paulo é de R$2.000,00.
- Qual a razão do salário de Pedro para o salário de Paulo? O que essa razão significa?
- Qual a razão recíproca do item acima? O que essa razão representa?
Atenção
É importante notar que, para se fazer a razão entre grandezas, estas devem estar na mesma unidade de medida.
Você lembra da capacidade de carga do caminhão no início do módulo?
Se a capacidade de carga desse caminhão é de 10 toneladas e cada caixa do produto que será transportado pesa 200kg, qual a razão entre o peso de cada caixa e a carga máxima transportada?
Como as cargas estão em unidades diferentes (uma está em toneladas e a outra está em kg), devemos colocá-las na mesma unidade. Como uma tonelada (1 ton) equivale a 1000kg, então a carga máxima do caminhão é de 10.000kg. Logo, a razão de 200kg para 10.000kg é:
Como veremos a seguir, é conveniente expressar a razão acima usando porcentagem.
Porcentagem
Porcentagem ou razão centesimal é o nome dado às razões cujo denominador é o número 100. Essas razões podem ser representadas pelo símbolo %.
Exemplo: 8% (lê-se: Oito por cento) é uma forma de representar a seguinte razão:
Em outras palavras, a expressão 8% significa que estamos tomando 8 partes de um todo que foi dividido em 100 partes iguais.
Vimos que a razão entre o peso de cada caixa e a carga máxima do caminhão era 0,02. Mas baseados na definição de porcentagem ou razão centesimal, esse valor simboliza o seguinte quociente:
Isso significa que a carga de cada caixa equivale a 2% da carga máxima do caminhão, ou seja, se considerarmos que o caminhão possui 100 espaços iguais, então cada caixa ocupa dois desses espaços.
Veja mais um exemplo no vídeo a seguir:
PROPORÇÃO
Uma proporção é o nome dado à igualdade entre razões. Dizemos que os números , , , , onde ≠ 0 e ≠ 0, formam, nessa ordem, uma proporção, se temos a seguinte igualdade:
Lê-se a expressão acima da seguinte maneira: está para , assim como está para .
Multiplicando ambos os termos da proporção por , obtemos . Este procedimento é chamado de multiplicação cruzada e é frequentemente utilizado em problemas envolvendo proporções.
Veja alguns exemplos de proporções:
A razão de 20 para 100 é 0,2, pois . A razão de 5 para 25 também é 0,2, pois . Assim, essas razões são iguais e podemos afirmar que a igualdade abaixo representa uma proporção:
Você já sabe: Tente resolver mais esses exemplos.
Sabendo que os números 20, 4, e 30 formam, nesta ordem, uma proporção, calcule o valor de .
Como os números 20, 4, e 30 formam, nesta ordem, uma proporção, podemos elaborar a seguinte igualdade de razões:
Fazendo a multiplicação cruzada obtemos:
A soma de dois números vale 700. Sabendo que um deles está para 3 assim como o outro está para 4, quanto vale o produto desses números?
Sejam e os números do enunciado. Como um deles, digamos , está para 3 assim como o outro está para 4, podemos formar a seguinte igualdade de razões:
Como sabemos que , temos que:
Agora, como e , então obtemos que . Logo, o produto desejado é:
Alguns dos principais problemas envolvendo proporções e porcentagens são resolvidos utilizando-se regras de três, como veremos no próximo módulo.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 3
Resolver problemas do cotidiano com regras de três
Introdução
Neste módulo, abordaremos o estudo e a resolução de problemas utilizando regras de três. Conforme veremos abaixo, existem diferentes tipos de regras de três e cada uma delas possui uma particularidade para a sua construção. Sendo assim, a eficácia desse método de solução depende estritamente desses detalhes que as diferenciam.
Antes de iniciarmos o estudo da regra de três, vamos relembrar os conceitos de grandezas diretamente proporcionais e de grandezas inversamente proporcionais. Estes conceitos serão o princípio básico para a resolução dos problemas envolvendo regras de três.
Duas grandezas são diretamente proporcionais quando, ao se multiplicar uma delas por um número positivo, a outra também é multiplicada por esse número. Duas grandezas são inversamente proporcionais quando, ao se multiplicar uma delas por um número positivo, a outra fica dividida por esse número.
Vejamos um exemplo prático para entendermos essa definição. Considere as seguintes situações:

Em uma fazenda, a produção mensal de laranjas é de 20 toneladas. Analisando as grandezas tempo de produção e peso de laranjas produzidas, vemos que essas grandezas são diretamente proporcionais, pois quando o tempo de produção dobra, o número de laranjas produzidas também dobra. Quando o tempo triplica, o número de laranjas também triplica, e assim por diante.

Dois operários levam 3 horas para descarregar um caminhão. Analisando as grandezas número de operários e tempo de descarregar, vemos que essas grandezas são inversamente proporcionais, pois dobrando o número de operários, o tempo para descarregar se reduz à metade. Triplicando o número de operários, o tempo se reduz à terça parte, e assim por diante.
Assista ao vídeo abaixo:
Vejamos agora como resolver problemas utilizando regras de três. Como temos três tipos distintos de regras de três, veremos cada um deles separadamente.
REGRA DE TRÊS SIMPLES E DIRETA
Utilizamos regra de três simples e direta quando queremos resolver problemas que envolvem duas grandezas que são diretamente proporcionais.
Vejamos alguns exemplos de resolução utilizando essa regra.
Em uma fazenda, a produção mensal de laranjas é de 20 toneladas. Qual é a produção anual em toneladas dessa fazenda?

Este é um típico caso de regra de três simples e direta.
Simples
Pois envolve apenas duas grandezas: tempo de produção e peso de laranjas produzidas.
Direta
Pois as grandezas envolvidas são diretamente proporcionais.
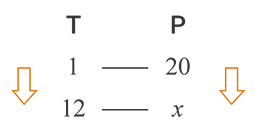
Vamos representar por T o tempo de produção (em meses) e por P a produção (em toneladas). Como 1 ano possui 12 meses, chamando de a produção desejada e utilizando os dados do enunciado, podemos fazer a seguinte representação:
As setas na figura acima apontam na mesma direção para significar que as grandezas são diretamente proporcionais.
Com essa orientação das setas, podemos montar a seguinte proporção:
E fazendo a multiplicação cruzada, obtemos que:
toneladas
Logo, a produção anual de laranjas dessa fazenda é de 240 toneladas.
O próximo exemplo é de um caso de regra de três simples envolvendo porcentagem. Você consegue resolver? Separe o material e vamos começar.
Anteriormente, vimos que o peso de uma caixa do produto equivale a 2% da carga máxima de um caminhão. Qual a quantidade máxima de caixas que o caminhão pode transportar?
Veja mais um exemplo de um caso de regra de três simples envolvendo porcentagem:
Renato, ao completar seus 18 anos, resolveu comprar seu primeiro carro.
Em uma revendedora de automóveis, o carro que ele mais gostou custa R$25.000,00.
Como Renato é muito convincente, combinou com o vendedor da loja o seguinte: Se o pagamento for em dinheiro, o valor do carro tem um desconto de 20%.
Qual é o valor do desconto desse carro no pagamento em dinheiro?
Regra de três simples inversa
Utilizamos regra de três simples inversa quando queremos resolver problemas que envolvem duas grandezas que são inversamente proporcionais.
Vejamos alguns exemplos de resolução utilizando essa regra.
Uma torneira leva 7 horas para encher um tanque. Se fossem utilizadas 5 torneiras, quanto tempo levaria para encher esse mesmo tanque?
Este é um caso de regra de três simples, pois envolve apenas duas grandezas: Tempo para encher e número de torneiras. Note também que essas grandezas são inversamente proporcionais, pois quando o número de torneiras é multiplicado por um fator, o tempo para encher o tanque é dividido por esse mesmo fator.
Vamos representar por T o tempo para encher (em horas) e por N o número de torneiras. Utilizando os dados do enunciado, podemos fazer a seguinte representação:
As setas na figura acima apontam em direções opostas para significar que as grandezas são inversamente proporcionais. Como a orientação das setas é oposta, antes de efetuar qualquer cálculo, devemos inverter os termos de uma das setas para que as duas setas apontem na mesma direção:
Agora, com essa orientação das setas, podemos montar a seguinte proporção:
E fazendo a multiplicação cruzada, obtemos que:
h
Como 1h = 60min:
h min min
Logo, 5 torneiras levariam para encher o tanque:
h h h hora e minutos
Pegue o papel e a caneta mais uma vez!
Agora você já consegue responder à questão apresentada no início do módulo.
Em uma transportadora, dois operários levam 3 horas para descarregar um caminhão. Quantas horas serão necessárias para 5 operários descarregarem esse caminhão?
Regra de três composta
Utilizamos regra de três composta quando queremos resolver problemas que envolvem três ou mais grandezas. Como temos mais do que duas grandezas envolvidas, a análise das grandezas em diretamente ou inversamente proporcionais deve ser feita aos pares, conforme veremos abaixo.

Em uma empresa de transporte, 10 trabalhadores descarregam 210 caixas de mercadoria em 3 horas. Quantas horas serão necessárias para 25 trabalhadores descarregarem 350 caixas?
Vamos praticar a regra de três composta:
(2013- BNDES) O gráfico abaixo apresenta o consumo médio de oxigênio, em função do tempo, de um atleta de 70kg ao praticar natação.
Considere que o consumo médio de oxigênio seja diretamente proporcional à massa do atleta. Qual será, em litros, o consumo médio de oxigênio de um atleta de 80kg, durante 10 minutos de prática de natação?
Vamos representar por M a massa do atleta (em kg), por L o consumo de oxigênio (em litros) e por T o tempo de atividade (em minutos). Pelo gráfico, podemos ver que um atleta de 70kg consome 21 litros de oxigênio em 4 minutos. Como queremos saber o consumo de um atleta com 80kg durante 10 minutos, podemos representar o problema da seguinte maneira:
Agora, vamos analisar se as grandezas são diretamente ou inversamente proporcionais.
Como queremos saber na grandeza L, vamos comparar as relações das grandezas M e T com relação a L.
- Considerando apenas as grandezas M e L, elas terão setas com orientação igual, pois, pelo enunciado, essas grandezas são diretamente proporcionais;
- Considerando apenas as grandezas T e L, elas terão setas com orientação igual também, pois, se aumentarmos o tempo de natação, aumentamos o consumo de oxigênio, ou seja, são grandezas diretamente proporcionais;
Como todas as setas apontam na mesma direção, então podemos montar a proporção que nos fornecerá o resultado desejado:
E fazendo a multiplicação cruzada, obtemos:
litros
Logo, um atleta com 80kg, durante 10 minutos de natação, consome 60 litros de oxigênio.
Atenção
É importante notar que a resolução da regra de três composta deve seguir os passos abaixo:
- A grandeza que contém a variável desejada ( no exemplo anterior está na grandeza T) deve ficar, preferencialmente, em um dos extremos (direita ou esquerda) para facilitar a visualização e auxiliar na proporção do cálculo final;
- Após analisar as orientações das setas e colocar todas no mesmo sentido, a proporção deve ser feita conforme visto nos exemplos acima, ou seja, a razão que contém a variável desejada (no caso, ) deve ficar isolada em um dos lados da igualdade, enquanto que as demais razões ficam do outro lado da igualdade sendo multiplicadas normalmente.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 4
Praticar problemas com juros simples e compostos
Introdução
Neste módulo, abordaremos um dos principais temas que se relacionam com empreendimentos financeiros (empréstimos, investimentos, aplicações, seguros, compras), que é o conceito de juro. Em cada situação, o juro pode representar uma situação diferente, por exemplo, o rendimento (ou lucro) de um investimento, imposto cobrado sobre um valor ganho (como a cobrança do imposto de renda), aumento no valor de uma compra (quando parcelamos) ou de uma conta (quando se atrasa o pagamento), desvalorização de um carro etc.
Considere a seguinte situação:

Ana pediu R$500,00 emprestados a Pedro, para pagar depois de 5 meses, à taxa de 3% ao mês. Qual será o valor que Ana deverá pagar ao final desse período?
Veremos que, para resolver esse problema, precisamos entender alguns fatores envolvidos nesse tipo de situação e saber qual espécie de juros está sendo cobrada: Simples ou composta.
Abaixo, apresentamos os principais conceitos que vamos precisar para o entendimento e estudo deste módulo.
Juro
Cujo símbolo será , é o nome dado a toda compensação em dinheiro que se paga ou que se recebe, por uma quantia de dinheiro que foi emprestada ou que se pede emprestada.
Capital
Essa quantia de dinheiro emprestada ou que se pede emprestada é chamada de capital,
cujo símbolo será
.
Taxa de porcentagem
A compensação que o juro fornecerá depende de uma taxa de porcentagem que irá ser paga ou recebida pelo empréstimo. Essa taxa é chamada de taxa de juro, cujo símbolo será .
Montante
O valor total em dinheiro que é pago ou recebido ao final do empréstimo (ou seja, capital + juro) é chamado de montante e é representado por .
Prazo
O tempo, do início ao término do empréstimo, é chamado de prazo, que denotaremos por .
A taxa de juros ( ) é indicada com relação ao intervalo de tempo, por exemplo: Dia, mês, ano, bimestre, trimestre etc. Abaixo, listamos os mais utilizados:
1% a.d.
Significa: 1% ao dia.
5% a.m.
Significa: 5% ao mês.
15% a.a.
Significa: 15% ao ano.
A taxa de juros ( ) e o tempo de aplicação (prazo = ) devem sempre estar na mesma unidade de medida, ou seja, se for uma taxa por dia, então deve ser contado em dias, se for uma taxa mensal, então deve ser contado em meses, e assim, sucessivamente.
Agora que sabemos todos os pré-requisitos para nosso estudo, vamos analisar os dois tipos de juros: Simples e composto.
Juros simples
Os juros simples são obtidos através do chamado regime de capitalização simples. Isso significa que não há incidência de juros sobre juros. Dessa forma, o juro obtido no regime de juros simples é o resultado da taxa de juros por período (que pode ser dias, meses, anos etc.) multiplicado pelo capital.
Voltemos ao exemplo de Ana: Qual será o valor pago a Pedro depois de 5 meses, considerando a taxa de 3% ao mês?
Vamos, inicialmente, extrair os dados do enunciado utilizando as notações já apresentadas.
- O capital emprestado foi = 500, a uma taxa de juros = 3% a.m., durante um período de = 5 meses.
Como a taxa é de 3% ao mês no regime de capitalização simples, então, ao final de cada mês, Ana deverá pagar juros de:
reais/mês
Sabendo que o empréstimo terá duração de = 5 meses, então, só de juros, Ana vai pagar:
math xmlns="https://www.w3.org/1998/Math/MathML">
J
=
5
×
15
=
75
Logo, ao final do período, Ana terá que pagar os R$500,00 acrescidos dos R$75,00 de juros, ou seja, Ana vai pagar R$575,00.
Note que, no exemplo acima, o valor pago de juros simples ao final do período de empréstimo foi determinado pela multiplicação:
Capital ( ) taxa ( ) tempo ( )
Ou seja, podemos representar os juros simples da seguinte maneira:
Considerando o valor do capital do empréstimo e a taxa de juros simples associada ao tempo de duração , o valor do juro simples será dado pela fórmula:
Ou simplesmente:
Dessa forma, o montante (valor total pago ou recebido do empréstimo) obtido ao final do período será dado por:
Vejamos mais alguns exemplos:
Maria aplicou R$10.000,00 à taxa de juros simples de 2% ao mês, durante 6 meses. Quanto Maria receberá de juros e de montante?
Temos que o capital inicial é = R$10.000,00, o tempo de aplicação é de = 6 meses e o juro simples é de:
ao mês
Como o tempo e a taxa de juros estão na mesma unidade de medida, então, utilizando a fórmula do juro simples, obtemos que:
E o montante será dado pela fórmula:
Outra forma para calcular o montante:
Logo, Maria receberá R$1.200,00 de juros e o montante será de R$11.200,00.
Note que, no exemplo acima, o tempo e a taxa de juros foram dados na mesma unidade de medida.
Como proceder no caso em que as unidades são diferentes?
Nesses casos, podemos utilizar regra de três simples e direta para igualarmos as unidades.
Utilizando essa informação, pegue papel e caneta e resolva mais esse exemplo.
Ana aplicou R$15.000,00 por 2 meses a uma taxa de juros simples de 36% ao ano. Qual foi o rendimento que Ana obteve ao final desse período?
Juros compostos
Os juros compostos são obtidos através do chamado regime de capitalização composta. Diferentemente do juro simples, nesse regime composto, significa que há incidência de juros sobre juros, ou seja, o juro de cada período é acrescentado ao capital, formando um novo capital. Sobre este novo capital incidem novos juros referentes ao período seguinte, e assim por diante. Esta é a situação que ocorre na maior parte das transações financeiras. Vejamos um exemplo para entendermos esse processo.
João aplicou R$300.000,00 em uma empresa a juro composto de 2% ao mês. Se a aplicação tiver duração de 3 meses, qual será o montante que João vai receber da empresa? De quanto foi o juro obtido após esse tempo?
Vamos, inicialmente, extrair os dados do enunciado utilizando as notações já apresentadas.
- O capital aplicado foi = 300.000, a uma taxa de juro composto de = 2% a.m. durante um período de = 3 meses.
Como no regime de juro composto ocorre incidência de juro sobre juro, para calcular o montante final, precisamos fazer o processo mês a mês, conforme mostramos abaixo.
João receberá de juros o equivalente a = 2% de = 300.000, ou seja, o juro obtido após o primeiro mês será:
Assim, o montante ao final do primeiro mês, que será o nosso novo capital (que denotaremos por 1), é de:
João receberá de juros o equivalente a = 2% de 1 = 306.000, ou seja, o juro obtido após o segundo mês será:
Assim, o montante ao final do segundo mês, que será o nosso novo capital (que denotaremos por 2), é de:
João receberá de juros o equivalente a = 2% de 2 = 312.120, ou seja, o juro obtido após o terceiro mês será:
Assim, o montante ao final do terceiro e último mês será:
Logo, o montante que João receberá da empresa ao final de 3 meses será de:
reais
O juro total obtido ao final do período é o valor do montante menos o valor do capital aplicado inicialmente, ou seja, o juro total obtido foi:
reais
Atenção
É necessário fazer este passo a passo sempre que trabalharmos com juros compostos?
A resposta é não. Este exemplo foi apenas para entendermos como o regime de juros compostos funciona. Para resolvermos esse tipo de problema, utilizamos a fórmula do montante para juro composto, apresentada abaixo.
Considerando o valor do capital aplicado (ou emprestado), a taxa de juros compostos associada ao tempo de duração , o valor do montante será dado pela fórmula:
Dessa forma, o juro obtido ao final do período será dado por:
Novamente, destacamos que, para efetuar esses cálculos, a taxa de juro e o tempo devem estar sempre na mesma unidade de medida, assim como vimos no cálculo do juro simples.
Baseado nas informações do exemplo de juros compostos, como o capital aplicado foi de = 300.000, a uma taxa de juro composto de ao mês, durante um período de = 3 meses, então, pela fórmula do montante, temos que o montante obtido por João ao final do terceiro mês de aplicação será:
reais
E o juro obtido será de:
reais
Outro caso possível para a utilização de juro (tanto o simples, quanto o composto) é o da desvalorização de um certo investimento, digamos, a desvalorização de um carro de acordo com o tempo.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
Conclusão
Considerações Finais
O estudante, em seu cotidiano, irá se deparar, com grande frequência, com os conceitos de Matemática apresentados neste tema. Por isso, os exemplos utilizados foram simples, diretos e realistas, procurando facilitar sua compreensão.
Nossa realidade econômica é complexa e instável e são comuns as ocorrências de confusão e de erros, tanto na assimilação da teoria quanto na prática dos cálculos. Uma vez bem informado — e seguro com isso —, o estudante estará apto a resolver os mistérios e dilemas matemáticos de seu dia a dia, dos pequenos aos grandes, podendo, assim, escapar de eventuais armadilhas criadas por si mesmo e pelos outros.
Podcast
CONQUISTAS
Você atingiu os seguintes objetivos:
Lorem ipsum dolor sit amet, consectetur adipiscing elit
Ut enim ad minim veniam, quis nostrud exercitation ullamco
Duis aute irure dolor in reprehenderit in voluptate velit esse